Эффект фрейминга
Эффект фрейминга (framing effect) – это
один из ключевых эффектов, которые изучает поведенческая
экономика. Заключается он в том, что если один и тот же
набор альтернатив описать по-разному, то и выбор человек
сделает неодинаковый.
Эффект фрейминга выявлен в исследованиях
основателей поведенческой экономики – Даниэля Канемана и
Амоса Тверски – американо-израильских психологов. Именно
в экспериментах, продемонстрировавших эффект фрейминга,
и был получены данные, которые (наряду с другими
данными) стали эмпирическим базисом теории перспектив
(prospect theory). Кстати, именно за разработку этой
теории Канеман и Тверски получили Нобелевскую премию по
экономике.
Конечно, зависимость от контекста, от
заданных рамок (frame в переводе с английского и
означает рамка) была хорошо известна в психологии и до
Канемана и Тверски. Примером тут может служить та же
иллюзия размера-веса (size-weight illusion), которую
открыл французский врач Огюстен Шарпатье (1852-1916) еще
в 1891 году. Иллюзия эта состоит в том, что если
предложить человеку определить, какой из двух имеющих
одинаковую массу предметов тяжелее (испытуемый,
естественно, о равенстве масс знать не должен), то более
тяжелым ему покажется тот, что имеет больший объем.
А вот еще более простой пример.
Взгляните на следующий рисунок:

В зависимости от того, вертикальный или
горизонтальный ряд вы рассматриваете, знак IЗ будет
восприниматься вами или как буква В (горизонтальный
ряд), или как цифра 13 (вертикальный ряд).
Впрочем, заслуга Канемана и Тверски
состоит в том, что они показали, каким образом рамки,
контекст, специфика формулировки оказывают влияние на
человека в ситуациях более важных, чем определение массы
предметов или чтение символов. Речь идет о ситуациях,
когда необходимо принять экономическое решение
(максимизировать пользу (доход) и минимизировать вред
(издержки)), сделать сложный выбор в условиях риска.
Вот вам пример.
Вы – глава одной из областей РФ. Этой
ночью ФСБ сообщила вам, что террористы нанесли по одному
из малых городов вашей области удар с помощью
биологического оружия – распылили смертоносные бактерии.
Население города составляет 6000 человек. Вы срочно
созываете эпидемиологов, чтобы выбрать оптимальный
способ защиты населения.
***
Читайте также по теме:
***
Вам предлагают выбрать одну из двух
разработанных эпидемиологами программ борьбы с
инфекцией: Программа "Гром" и Программа "Град".
Причем эпидемиологи вычислили, что
Программа "Гром" позволит гарантированно спасти 2000
человек, тогда как Программа "Град" с вероятью один шанс
из трех спасет всех жителей города, но с вероятностью
два шанса их трех не спасет никого.
Какую программу вы предпочтете?
Обязательно сделайте выбор, причем
зафиксируйте его письменно.
И еще пример.
Через год террористы снова атаковали
один из городов. Его население также составляет 6000
человек. И эпидемиологи вновь предлагают вам выбрать
одну из двух программ противодействия заражению:
Программа "Шторм" – гарантированно
погибнут 4000 человек.
Программа "Вихрь" – один шанс из трех,
что никто не погибнет, но два шанса из трех, что
погибнут все.
Какую программу вы предпочтете?
Обязательно сделайте выбор и
зафиксируйте его письменно.
Думаю, в первом случае вы остановились
на программе "Гром". Во всяком случае именно такой выбор
сделало большинство испытуемых в соответствующих
экспериментах. И в этом выборе, определенно, есть
логика. Зачем рисковать, пытаясь спасти всех, когда
можно гарантированно спасти целых 2000 человек?
Ну, а во втором случае вы, должно быть,
выбрали программу "Вихрь". И это, опять-таки, вполне
логично и соответствует выбору большинства. Чем
смириться с гибелью четырех тысяч ни в чем не повинных
людей, лучше использовать хотя и незначительный, но все
же шанс на спасение.
Так в чем же проявился эффект фрейминга?
Да вот именно в описанной архитектуре
выбора! Дело в том, что Программа "Гром" по своему
эффекту полностью идентична программе "Шторм". Так что,
если уж в первой ситуации вы предпочли смириться с
гибелью четырех тысяч человек, не понятно, почему вы
решили проявить некое милосердие во второй ситуации.
Программа "Вихрь" также совершенно тождественна
программе "Град".
Не верите? Тогда взгляните на
следующие таблицы:
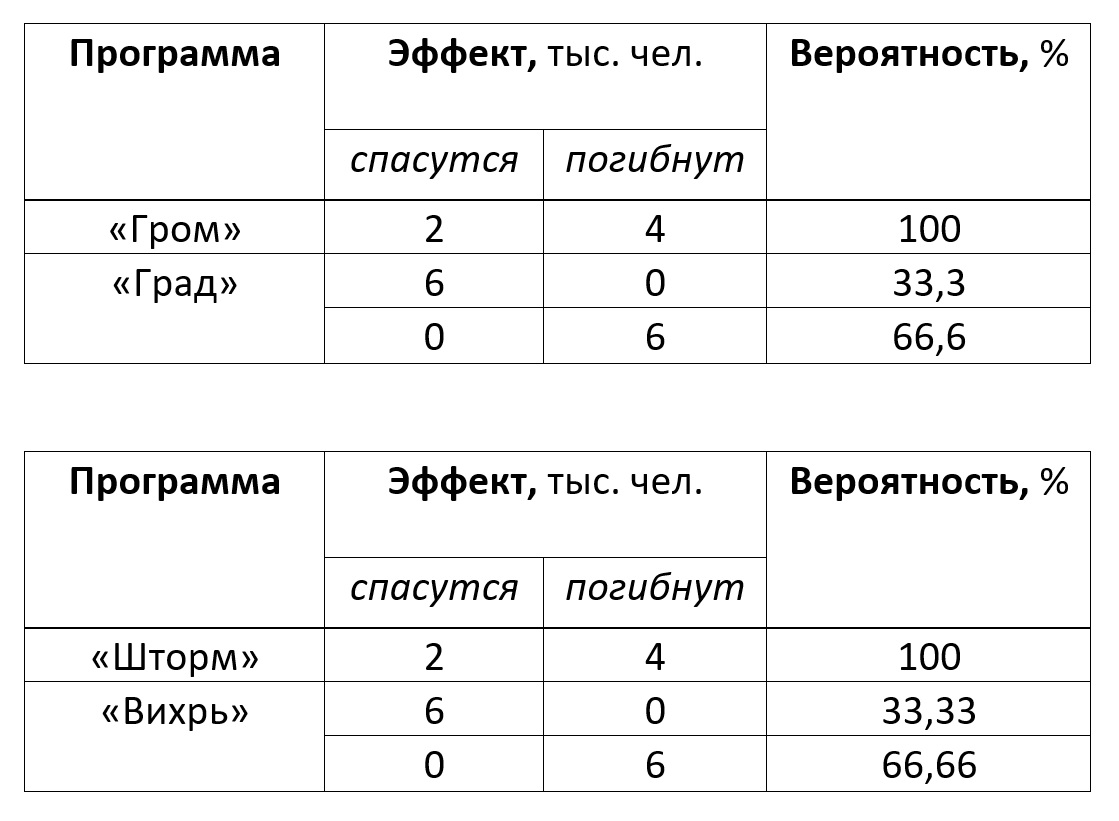
Чем отличаются эти таблицы? Только
названиями программ.
Фрейминг, который применен в этих
ситуациях, носит наименование "фрейминг исходов" (framing
of outcomes).
В данном случае есть два исхода:
"спасение" и "гибель". Гарантированное спасение
заставляет нас избегать риска. Тогда как гарантированная
гибель, наоборот, подталкивает к риску.
В целом фрейминг исходов – это описание
исхода как позитивного или негативного, как приобретения
или потери, как выигрыша или проигрыша.
Вероятности аналогичных исходов при этом
виде фрейминга остаются неизменными. И вы можете
убедиться в этом, взглянув на последние столбцы
приведенных таблиц.
Но что будет, если мы, не станем
описывать аналогичные исходы по-разному, но зато изменим
вероятности их наступления?
В этом случае будет иметь место так
называемый "фрейминг вероятностей" (framing of
contingencies).
Давайте же посмотрим на него
повнимательнее, решив следующие задачи.
Задача 1
Выберите, что вы предпочтете?
Получить 3000 рублей.
Сыграть в следующую игру. Перед вами
пять карт рубашкой вверх. Вы знаете, что это четыре туза
и пиковая дама. Вам нужно будет выбрать одну карту. Если
это будет туз, вы получите 4500 рублей, если пиковая
дама – вы не получите ничего.
Задача 2
Выберите, в какую игру сыграть:
Перед вами четыре карты рубашкой вверх.
Это три шестерки и туз. Вы должны выбрать одну карту.
Если это будет туз, вы выиграете 3000 рублей.
Перед вами пять карт рубашкой вверх. Это
четыре шестерки и туз. Вы должны выбрать одну карту.
Если это будет туз, вы выиграете 4500 рублей.
Задача 3
Вам предстоит сыграть в следующую игру.
Перед вами четыре карты рубашкой вверх. Это три шестерки
и туз. Вы выбираете карту. Если это будет туз, то у вас
появятся две возможности:
Получить 3000 рублей.
Перед вами выложат пять карт. Это будут
четыре туза и пиковая дама. Вы сможете выбрать одну
карту. Если окажется, что это туз, вы получите 4500
рублей.
Причем выбор вы должны сделать до того,
как начнете играть.
Пожалуйста, сделайте выбор в каждой из
этих и запишите его, прежде чем двигаться дальше.
В первой задаче большинство испытуемых
предпочитают вариант А. И правда, как-то не хочется
рисковать, пытаясь выиграть больше, если можно получить
хотя и меньшие деньги, но зато гарантированно.
Такой выбор вписывается в присущее нам
когнитивное искажение под названием "предпочтение
нулевого риска".
Во второй задаче большинство
предпочитает вариант В. И это совершенно правильное с
экономической точки зрения решения. Действительно, чтобы
сделать правильный выбор, нужно смотреть не просто на
размер выигрыша, но и на вероятность его получения. Это
означает, что необходимо подсчитать математическое
ожидание – умножить размер выигрыша на вероятность его
получения.
Давайте сделаем это.
В варианте 2А у нас есть один шанс из
четырех выиграть 3000 рублей. Математическое ожидание в
этом случае таково:
0,25 * 3000 = 750
В варианте 2В вероятность выигрыша ниже
– один шанс из пяти. Зато выигрыш больше – целых 4500.
Подсчитаем матожидание:
0,2 * 4500 = 900
Как видим, рациональнее выбрать вариант
2В.
Но дело в том, что и в задаче 1 более
рациональным является выбор варианта В, тогда как
большинство выбирает вариант А.
Такое изменение предпочтений из-за
изменения вероятностей исходов – предпочтение менее
вероятного исхода, когда вероятности низкие, и
предпочтение более вероятного исхода, когда вероятности
высокие – носит наименование "эффект определенности"
(certainty effect).
Так же различия в решениях задачи 1 и
задачи 2 является одним из примеров парадокса Алле.
Но мы еще не рассмотрели задачу 3.
Давайте же сделаем это.
В этой задаче большинство выбирает
вариант А, и это ошибочное решение. Почему?
Да потому, что, фактически, в этой
задаче нам предлагают игру в два тура, которые маскируют
от нас подлинные вероятности выигрышей. Поэтому в задаче
3 мы принимаем то же решение, что и в задаче 1, хотя эти
задачи отличаются принципиально: вариант 1А – это
выигрыш с вероятность 100%, тогда как вариант 3А – это
выигрыш с вероятностью всего лишь 20%.
Как мы получили эту вероятность?
Давайте посмотрим на следующую схему:
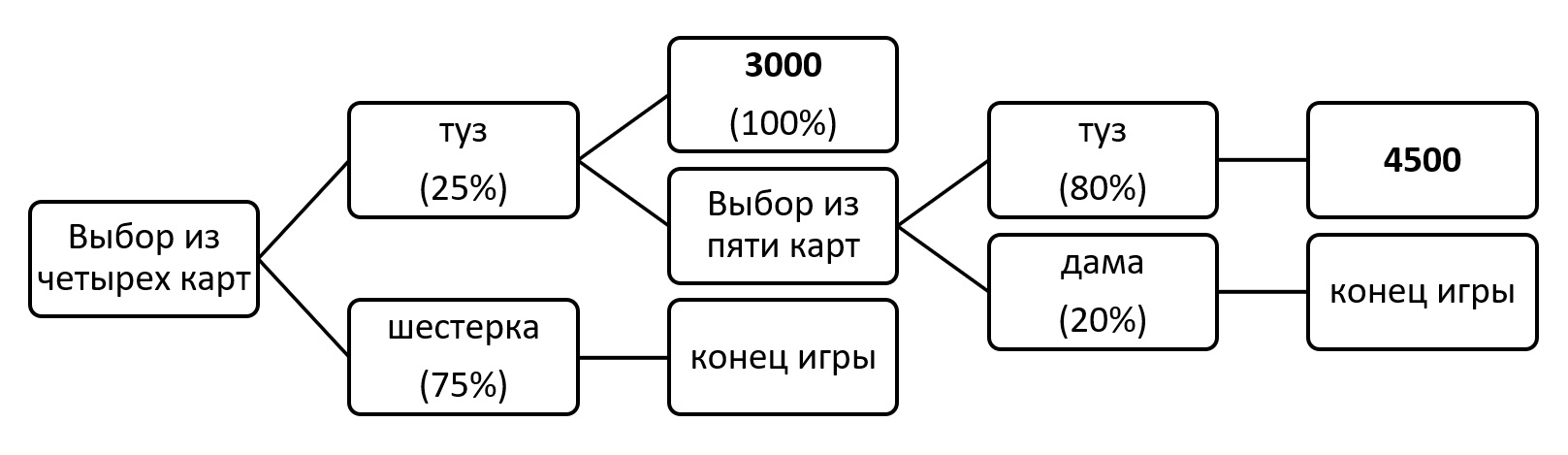
Как видим, и вероятность получения 3000
рублей, и вероятность получения 4500 рублей должна
рассматриваться сквозь призму 25%-ой вероятности того,
что при первом выборе карты вам выпадет туз. В такого
рода случаях вероятности необходимо перемножить.
Давайте сделаем это.
Вариант 3А: 0,25*1 = 0,25
Вариант 3В: 0,25*0,8 = 0,2
Если теперь мы подсчитаем математические
ожидания, то увидим, что они совпали с матожиданиями
исходов задачи 2:
Вариант 3А: 0,25 * 3000 = 750
Вариант 3В: 0,2 * 4500 = 900
А это означает, что предпочтение
большинством варианта 3А является нерациональным.
Такого рода нерациональное поведение –
выбор в ситуации низких вероятностей совпадает с выбором
в ситуации высоких вероятностей – обозначается термином
"эффект мнимой определенности" (pseudocertainty effect).
Таким образом, можно выделить два вида
фрейминга:
1. Фрейминг исходов.
2. Фрейминг вероятностей: эффект
определенности и эффект мнимой определенности.
Почему же существует эффект фрейминга?
Канеман и Тверски для ответа на этот
вопрос вводят понятие "неприятие потерь" (loss
aversion). Они утверждают, что именно неприятие потерь
заставляет человека принимать разные решения в одной и
той же ситуации в зависимости от того, описана она в
терминах выигрышей, приобретений, доходов или в терминах
проигрышей, потерь, расходов. К сожалению, неприятие
потерь постепенно стали трактовать расширительно, начали
предлагать его зоологические и эволюционные
интерпретации. Тем не менее, следует понимать, что
неприятие потерь – это не эмпирический феномен, а
теоретический конструкт, на котором строится
объяснительный принцип.
Александр Невеев
Примечание
Kahneman, D., Tversky, A. (1984).
Choices, values, and frames. American
Psychologist, 39 (4): 341-350.
Tversky, A.,
Kahneman, D. (1981). The Framing of decisions and the
psychology of choice. Science, 211 (4481):
453–458.
|

